Solar System Dynamic Wallpaper

Idea:

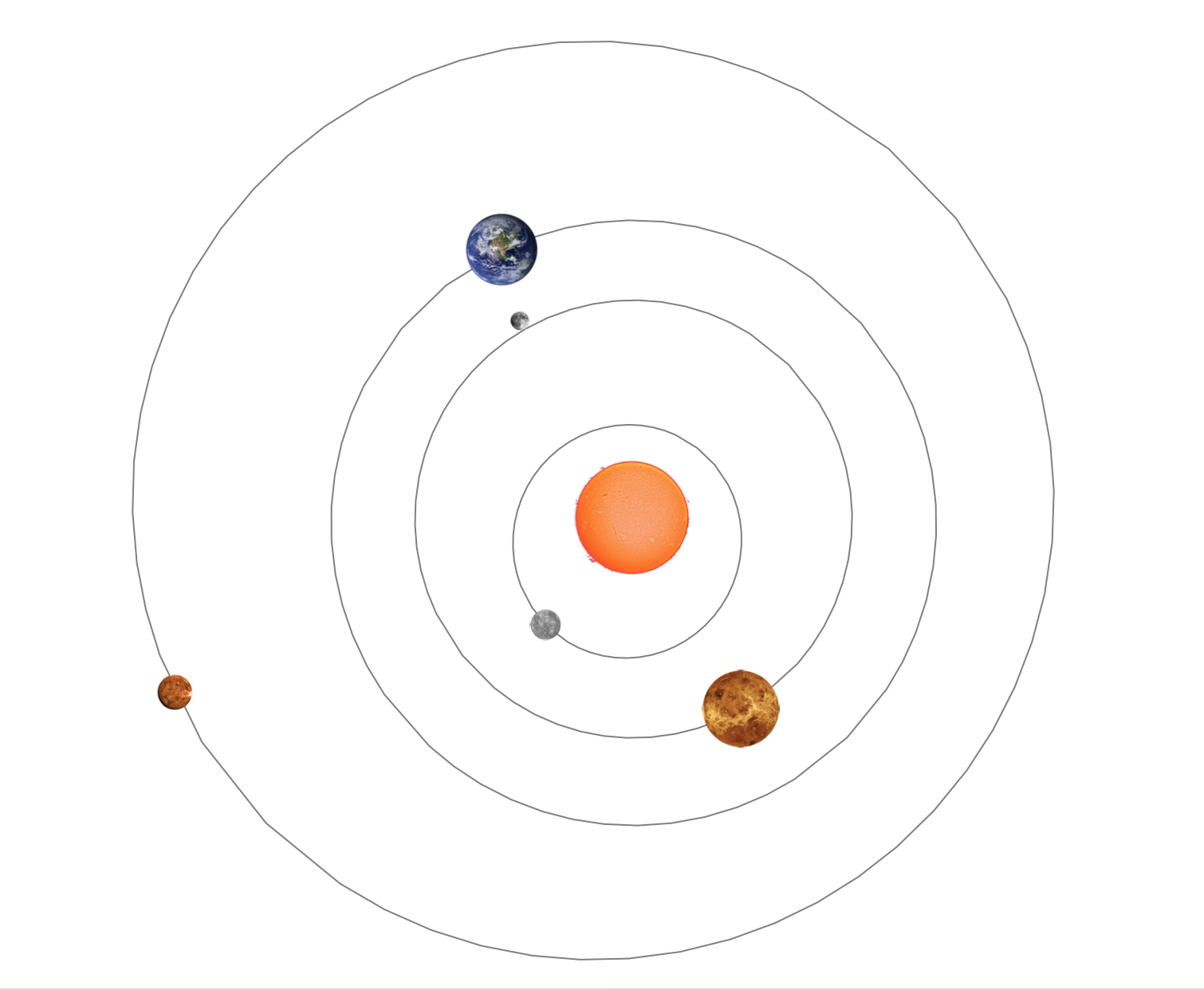
I love the idea of how all the planets interact with each other and with the sun. So, I wanted to produce a real-time map of the solar system, updated every 5-10 seconds, with various statistics shown in the top corner. In addition, I'm excited about calculating how the sun's light bounces around the solar system and ends up back at Earth. This would be an imitation of the dynamic backgrounds capable in Windows and Linux distros. It is possible that I may just want to switch over to Linux, but for now, I'll just find (hacky and inefficient) ways to implement the same functionality on macOS. Currently macOS is so bent on optimizing the desktop image, that I am forced to generate a new image file, each time with a randomized end, ex: img438724023.png. Otherwise the OS wont update the picture each time the planets move.

I may be updating this project as time passes, due to its presense on my desktop. I may just look at it one day and decide I want a certain statistic. This project wont really ever be truly over.

Screenshot of my desktop today (Jan 15 2018):

Current Statistics:

* Distance to all other planets / Angles in the sky from us to those planets
* Gravitational force experienced by each planet based on your current latitude/longitude and time of day
* Current time until we actual get humans to Mars (final date will be updated manually as I read the news). Will remain up there because I want to remind myself about it and stay hopeful.
* Moon phase
* Current orbital speed of the Earth around the Sun and the Moon around the Earth (these change regularly).

Planned Statistics:

* Light received from each planet. I can do this from the Sun easily, but it takes a few more steps to calculate relative directions and how much light will bounce to Earth. * Tide info * A dynamic set of events and times till events that automatically update based on a public repository somewhere.

Background:

Many of the statistics are collected through Mathematicas built in data retrieval tools. They are then interpreted visually and calculations are performed based off of them. One of these is "Position." I can simply call a built in function and get the position of the Astronomical body at any time. It is handy and allows me to not have to reinvent the wheel.

Here is an image of the solar system module before being transposed with other statistics:

Here is a video of the physics simulator being let free to play with equations as time passes. I find it kind of interesting but not incredibly visually appealing:

Sourcecode for the simulator, not the data gathering tools:
(planet-names originate from Kerbal Space Program)

		(*Data Management Tools*)
\
(*$PreRead=(#/.s_String/;StringMatchQ[s,NumberString]&&Precision@\
ToExpression@s\[Equal]MachinePrecision\[RuleDelayed]s<>"`25."&);*)
\
ClearAll[withRules]
SetAttributes[withRules, HoldAll]
withRules[rules_, expr_] := 
 First@PreemptProtect@
   Internal`InheritedBlock[{Rule, RuleDelayed}, 
    SetAttributes[{Rule, RuleDelayed}, HoldFirst];
    Hold[expr] /. rules]
set[paramList_, newRules_] := 
 DeleteDuplicates[Join[newRules, paramList], First[#1] === First[#2] &]
set1[paramList_, newRules_] := 
 DeleteDuplicates[Join[{newRules}, paramList], 
  First[#1] === First[#2] &]
(*Structs*)

particleStruct = {name -> "particle", type -> 0, charge -> 0, 
   mass -> 0, radius -> 0, position -> {x, y, z}, 
   velocity -> {x, y, z}, cforce -> {0, 0, 0}};
createparticle[dname_, dtype_, dcharge_, dmass_, dradius_, dposition_,
   dvelocity_] := (
  set[{}, {name -> dname, type -> dtype, charge -> dcharge, 
    mass -> dmass, radius -> dradius, position -> dposition, 
    velocity -> dvelocity, cforce -> {0, 0, 0}}])
getPosX[p_] := withRules[p, position[[1]]]
getPosY[p_] := withRules[p, position[[2]]]
getPosZ[p_] := withRules[p, position[[3]]]
setPosX[p_, val_] := (pos = withRules[p, position];
  pos[[1]] = val;
  set1[p, position -> pos])
setPosY[p_, val_] := (pos = withRules[p, position];
  pos[[2]] = val;
  set1[p, position -> pos])
setPosZ[p_, val_] := (pos = withRules[p, position];
  pos[[3]] = val;
  set1[p, position -> pos])
timeIncS = 100000;

getVelX[p_] := withRules[p, velocity[[1]]]
getVelY[p_] := withRules[p, velocity[[2]]]
getVelZ[p_] := withRules[p, velocity[[3]]]


updateVels[particles_] := 
 Table[set1[particles[[p]], 
   velocity -> 
    timeIncS*((cforce /. particles[[p]])/(mass /. 
         particles[[p]])) + (velocity /. particles[[p]])], {p, 
   Length[particles]}]
updatePositions[particles_] := 
 Table[set1[particles[[p]], 
   position -> 
    timeIncS*(velocity /. particles[[p]]) + (position /. 
       particles[[p]])], {p, Length[particles]}]

orbitalDirectionalVel[mass_, dist_] := Sqrt[constOfG*(mass)/dist]
constOfG = 6.67408*10^-11
calcGravForce[p1_, p2_] := -1*((position /. p1) - (position /. p2))/
  Total[Abs[((position /. p1) - (position /. p2))]]*
  constOfG*((mass /. p1)*(mass /. p2))/
  Total[((position /. p1) - (position /. p2))^2]
calculateGravitationalForceNewtons[particles_] := (
  Table[set1[particles[[p]], 
    cforce -> ((calcGravForce[particles[[p]], #] &) /@ 
        Select[particles, ! (# === particles[[p]]) &] // Total)], {p, 
    Length[particles]}]
  )
bouncyForce[particles_] := (
  Table[set1[particles[[p]], 
    cforce -> (cforce /. 
        particles[[p]]) - ((calcGravForce[particles[[p]], #] &) /@ 
         Select[particles, ! (# === particles[[p]]) &] // Total)], {p,
     Length[particles]}]
  )
  
  particlePlot3D[particles_] := (
  Graphics3D[{
    (*particles themselves*)
    
    Sphere[position /. particles, radius /. particles],
    (*particle Names*)
    
    Table[Text[(name /. particles)[[p]]], {p, Length[particles]}]}])
particleTracing[particlesV_, timeSeconds_] := (
   particles = particlesV;
   data = Table[(
      particles = calculateGravitationalForceNewtons[particles];
      particles = updateVels[particles];
      particles = updatePositions[particles];
      
      particles
      ), {graphically, timeSeconds/timeIncS}];
   
   ListPlot[
    Flatten[Table[(position /. data)[[All, n]], {n, 
        Length[particles]}], 1][[All, 1 ;; 2]], PlotRange -> All]
   );

calculatePlanetaryForceString[planetother_, positions_] := (
   posSelf = 
    Flatten[positions[[
       Flatten[Position[planets, _?(# == "Earth" &)]]]]]/
     Quantity[1, "Meters"];
   posSelf[[1]] += 6.7*10^6;
   occurences = Flatten[Position[planets, _?(# == planetother &)]];
   posPlanetOther = 
    If[Length[occurences] == 1, 
     Flatten[positions[[occurences]]]/Quantity[1, "Meters"], 
     AstronomicalData[planetother, "Position"]/
      Quantity[1, "Meters"]];
   massPlanetOther = 
    AstronomicalData[planetother, "Mass"]/Quantity[1, "Kilograms"];
   
   particleSelf = 
    createparticle["particleSimSelf", 0, 0, 68, 0, posSelf, {0, 0, 0}];
   particlePlanet = 
    createparticle["particleSimOtherPlanet", 0, 0, massPlanetOther, 0,
      posPlanetOther, {0, 0, 0}];
   
   forceVector = calcGravForce[particleSelf, particlePlanet];
   force = Abs[Total[forceVector]];
   
   
   planetOtherAltitude = 
    AstronomicalData[planetother, "Altitude"] /
     Quantity[1, "AngularDegrees"];
   planetOtherAzimuth = 
    AstronomicalData[planetother, "Azimuth"]/
     Quantity[1, "AngularDegrees"];
   
   azimuthWord = "";
   If[(planetOtherAzimuth > 330 || planetOtherAzimuth < 30), 
    azimuthWord = "North"];
   If[(30 < planetOtherAzimuth < 60), azimuthWord = "North-East"];
   If[(60 < planetOtherAzimuth < 120), azimuthWord = "East"];
   If[(120 < planetOtherAzimuth < 150), azimuthWord = "South-East"];
   If[(150 < planetOtherAzimuth < 210), azimuthWord = "South"];
   If[(210 < planetOtherAzimuth < 240), azimuthWord = "South-West"];
   If[(240 < planetOtherAzimuth < 300), azimuthWord = "West"];
   If[(300 < planetOtherAzimuth < 330), azimuthWord = "North-East"];
   azimuthWord;
   
   altitudeWord = "";
   If[0 < planetOtherAltitude, altitudeWord = "Up", 
    altitudeWord = "Down"];
   altitudeWord;
   
   returnString = 
    ToString[force, FormatType -> TraditionalForm] <> " Newtons at " <> 
     ToString[planetOtherAzimuth ] <> "˚ " <> azimuthWord <> ", " <> 
     ToString[planetOtherAltitude] <> "˚ " <> altitudeWord);
dLightMinutesString[
   planet_] := (ToString[(AstronomicalData[planet, 
       "DistanceLightYears"]/Quantity[1, "LightMinutes"])]);
       
       mathTesting[] := (
   simTime = 1;
   p1 = createparticle["Sol", 0, 
       0, (1.98855*10^30), (6.7*10^8), {0, 0, 0}, {0, 0, 0}]
      p2 = 
     createparticle["Earth", 0, 0, 
        5.972*10^24, (6.371*10^8), {(149.6*10^9), 0, 0}, {0, 
         orbitalDirectionalVel[(mass /. p1), (149.6*10^9)], 0}]
       p3 = 
      createparticle["Eloo", 0, 0, 0.1, 
         3, {100, 10, 0}, {orbitalDirectionalVel[(mass /. p2), 10], 
          orbitalDirectionalVel[(mass /. p1), 100.5], 0}]
        p4 = 
       createparticle["Jool", 0, 0, 2, 
          5, {-100, 0, 
           0}, {0, -orbitalDirectionalVel[(mass /. p1), 100], 0}]
         p5 = 
        createparticle["Duna", 0, 0, 0.1, 
          3, {-100, -10, 
           0}, {-orbitalDirectionalVel[(mass /. p4), 
             10], -orbitalDirectionalVel[(mass /. p1), 100.5], 0}]
         particles = {p1, p2};
   Sqrt[constOfG*(mass /. p2)/15] // N
     particlePlot3D[particles]
     particleTracing[particles, simTime]
     
     timeIncS = 1;
   vid = Table[(
      particles = calculateGravitationalForceNewtons[particles];
      particles = updateVels[particles];
      particles = updatePositions[particles];
      
      particlePlot3D[particles]
      ), {graphically, ((simTime)/timeIncS)}];
   ListAnimate[vid];
   );

t1 = AbsoluteTime[]
planets = {"Mercury", "Venus", "Earth", "Moon", "Mars", "Sun"};
positions = Map[AstronomicalData[#, "Position"] &, planets];
distances = 
  Table[Sqrt[(Total[positions[[p]] - positions[[3]]]^2)], {p, 
    Length[planets]}];
data = (positions[[All, 1 ;; 2]])/Quantity[1, "Meters"];
data[[4]] = ((90*(data[[4]] - data[[3]])) + data[[3]]);
maxNumber = Max[Abs[Flatten[data]]];
td = AbsoluteTime[] - t1;
Print["Loading " <> ToString[td]];
t1 = AbsoluteTime[];

planetarysizequotient =  75000;
imagesizedata = {2440, 6052, 6371, 1737, 3390, 9500}/
   planetarysizequotient;
imagedata =  
  Import[#] & /@ \
("/Users/Zack/Tools/Programming/Mathematica/ImagesOfPlanets/" <> # & \
/@ (# <> "LQ.png" & /@ planets));
pathdata = 
  Map[AstronomicalData[#, "OrbitPath"][[All, All, 1 ;; 2]] &, 
    planets] // DeleteMissing;
pathdata = 
  Table[Line[Level[pathdata[[p]], 1]*1.496*10^11 / maxNumber], {p, 1, 
    Length[pathdata]}];
data = data/maxNumber;

td = AbsoluteTime[] - t1;
Print["Loading2 " <> ToString[td]];
t1 = AbsoluteTime[];

solarSystemView = Show[
   Graphics[{Gray, pathdata}],
   Graphics[
    Table[{Red, Glow[Red], 
      Inset[imagedata[[p]], data[[p]], Center, 
       Scaled[{imagesizedata[[p]], imagesizedata[[p]]}]]}, {p, 1, 
      Length[data]}]],
   ImageSize -> {1200, 600}
   ];
td = AbsoluteTime[] - t1;
Print["Solar System Img Gen " <> ToString[td]];
t1 = AbsoluteTime[];

backgroundImage = Show[
   Graphics[{White, Text[Style["
                
                Live Statistics:
                Gravitational force experienced by:
                    Sun: " <> 
        calculatePlanetaryForceString["Sun", positions] <> "
                    Moon: " <> 
        calculatePlanetaryForceString["Moon", positions] <> "
                    Mars: " <> 
        calculatePlanetaryForceString["Mars", positions] <> "
                    Mercury: " <> 
        calculatePlanetaryForceString["Mercury", positions] <> "
                    Venus: " <> 
        calculatePlanetaryForceString["Venus", positions] <> "
                    Jupiter: " <> 
        calculatePlanetaryForceString["Jupiter", positions] <> "
                    Milkyway: " <> 
        calculatePlanetaryForceString["MilkyWay", positions] <> "
                
                Moon Phase: " <> 
        Capitalize[
         ToString[MoonPhase["Name"], FormatType -> TraditionalForm]] <>
         "
                Current speed of Earth around Sun: " <> 
        ToString[AstronomicalData["Earth", "Speed"], 
         FormatType -> TraditionalForm] <> "
                
                Time for light to travel to each object (from Earth):
                	Sun: " <> dLightMinutesString["Sun"] <> " minutes
                	Moon: " <> dLightMinutesString["Moon"] <> " minutes
                	Mars: " <> dLightMinutesString["Mars"] <> " minutes
                	Mercury: " <> dLightMinutesString["Mercury"] <> 
        " minutes
                	Venus: " <> dLightMinutesString["Venus"] <> 
        " minutes
                	Jupiter: " <> dLightMinutesString["Jupiter"] <> 
        " minutes
                
                Time till we reach Mars (updated with news):
                	Date: Unknown, \"2022\" 
                	Days till date: " <> 
        ToString[DateDifference[Today, DateObject[{2022, 1, 1}]]] <> 
        "
                ", TextAlignment -> Left, Medium], {1.7, .2}], White, 
     Text[Style["Zachary A Porter", FontFamily -> "Atlantis Found", 
       TextAlignment -> Right, Large], {1.6, -1}]}],
   
   
   
   solarSystemView,
   Background -> Black,
   ImageSize -> {1200, 600}
   ];
td = AbsoluteTime[] - t1;
Print["Background Gen " <> ToString[td]];
t1 = AbsoluteTime[];
backgroundImage = Rasterize[backgroundImage, RasterSize -> 3200]
num = RandomInteger[{1, 10^8}];
td = AbsoluteTime[] - t1;
Print["Background Raster " <> ToString[td]]
t1 = AbsoluteTime[];
Export[("/Users/Zack/backgroundImage/img" <> ToString[num] <> ".png"),
   backgroundImage, ImageSize -> 3200];
td = AbsoluteTime[] - t1;
Print["Exporting " <> ToString[td]];
t1 = AbsoluteTime[];

lightEnergyReceivedEXPERIMENTAL[] := (planetOther = "Earth"
      planetOther2 = "Sun"
       myLatitude = 47.6062
       myLatitudeRadians = myLatitude*Pi/180;
   distanceP1SunVec = 
    Abs[AstronomicalData[planetOther2, "Position"] - 
       AstronomicalData[planetOther, "Position"]]/
     Quantity[1, "Meters"];
   distanceP1SunScalar = Sqrt[Total[distanceP1SunVec^2]];
   energyDispersionFactor = (4 Pi*distanceP1SunScalar^2)^-1;
   angularSize = 
    2*(180/Pi)*
     ArcTan[(AstronomicalData[planetOther2, "Radius"]/
         Quantity[1, "Meters"])/distanceP1SunScalar];
   wattsProducedBySun = 3.86*10^26
      energyPerM2Equator = energyDispersionFactor*wattsProducedBySun
       planetaryEnergyDistributionCurve[x_] := 1/Sqrt[1 - x^2]
        myHeight = Sin[myLatitudeRadians]
         myPercentEnergy = 1/planetaryEnergyDistributionCurve[myHeight]
          myNoonGeneralEnergy = myPercentEnergy*energyPerM2Equator
           myAximuth = 
          
          AstronomicalData[planetOther2, "Altitude"]/
             Quantity[1, "AngularDegrees"]
            planetOther2Height = Sin[myAximuth*Pi/180]
             myCurrentPercentEnergy = 
            If[planetOther2Height > 0, 
               1/planetaryEnergyDistributionCurve[planetOther2Height],
                0]
              myCurrentEnergyFromP2 = 
             myCurrentPercentEnergy*energyPerM2Equator
   );